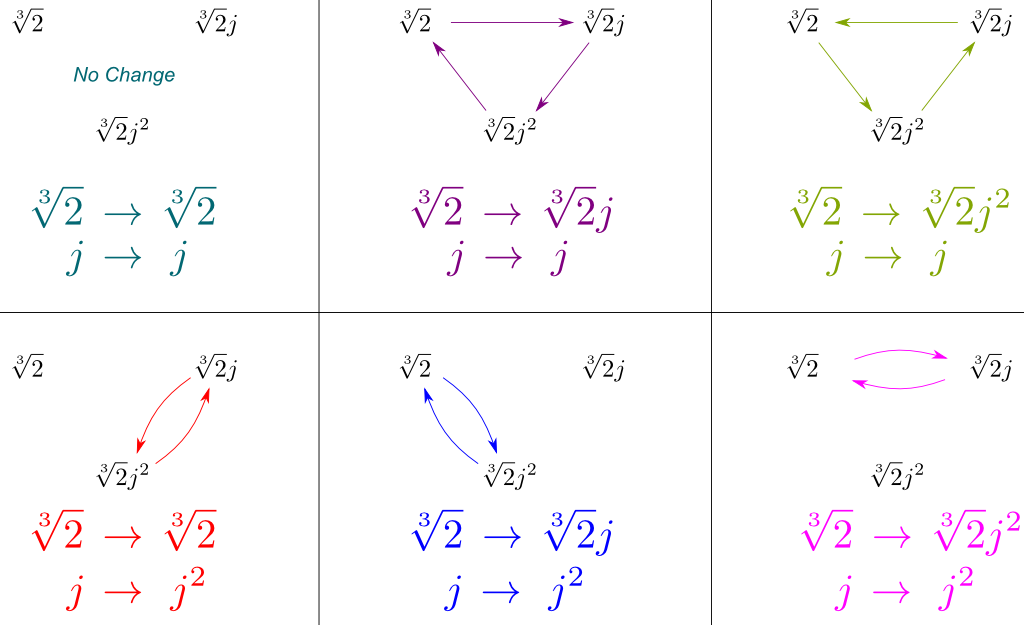List of the Greatest Mathematicians ever and their Contributions



This note explains the following topics: Simple groups, Examples of groups, Group actions, Sylow’s Theorem, Group extensions, Soluble and nilpotent groups, Symmetric and alternating groups, Linear groups.
Chapter 1 GroupTheory Most lectures on group theory actually start with the definition of what is a group. It may be worth though spending a few lines to mention how mathe-
Galois theory for beginners: A Historical Perspective. Jörg Bewersdorff. Download of excerpts as ebook
Examples with Intermediate Values. The following is a list of algorithms with example values for each algorithm. This list may not always accurately reflect all …
Group Action. A group is said to act on a set when there is a map such that the following conditions hold for all elements .. 1. where is the identity element of .. 2. for all .
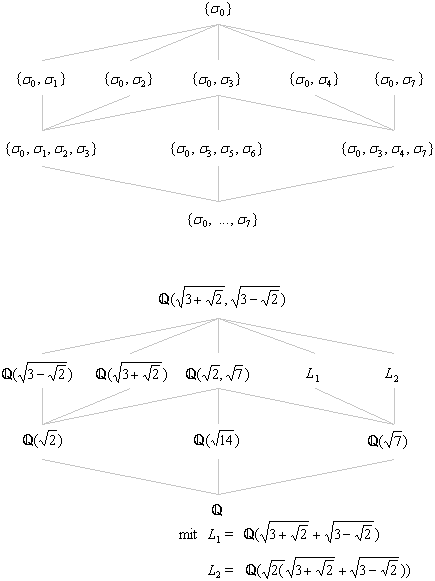
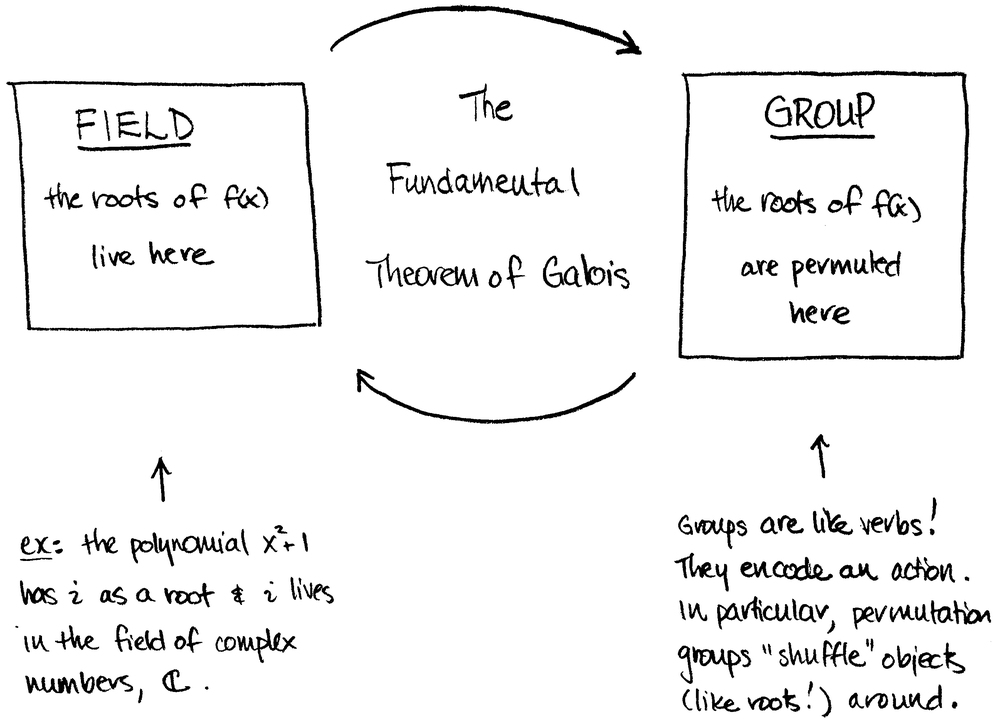
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory.Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood.
Effective polynomial representation. The finite field with p n elements is denoted GF(p n) and is also called the Galois Field, in honor of the founder of finite field theory, Évariste Galois.

CHAPTER 1 Basic Definitions and Results The axioms for a group are short and natural. Yet somehow hidden behind these axioms is the monster simple group, a huge and extraordinary
These notes give a concise exposition of the theory of fields, including the Galois theory of finite and infinite extensions and the theory of transcendental extensions.